บทที่5
..สมการกำลังสอง (quadratic equations) คือ สมการของพหุนามตัวแปรเดียวที่มีดีกรีเท่ากับ 2 บางครั้งเรียกสมการกำลังสองว่า สมการดีกรี 2 รูปแบบทั่วไปของสมการกำลังสอง คือ
…………………….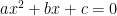
….. เมื่อ เป็นค่าคงตัว และ
เป็นค่าคงตัว และ 
…………………….
….. เมื่อ
…..การแก้สมการกำลังสอง หมายถึง การคำนวณเพื่อหาค่าของตัวแปร ซึ่งจะได้ค่าตัวแปร 2 ค่า โดยค่าทั้งสองอาจเท่ากันหรือไม่เท่ากันก็ได้ ค่าของตัวแปรที่ได้บางครั้งเรียกว่า รากของสมการหรือ คำตอบของสมการ
…..วิธีแก้สมการกำลังสอง ก่อนที่จะทำการคำนวณหาค่าตัวแปรของสมการกำลังสอง ให้จัดขวามือของเครื่องหมายเท่ากับให้เป็น 0 แล้วการคำนวณจะมีได้ 3 วิธี คือ โดยวิธีแยกตัวประกอบ โดยวิธีทำให้เป็นกำลังสองสมบูรณ์ และโดยวิธีใช้สูตร
…..วิธีแก้สมการกำลังสอง ก่อนที่จะทำการคำนวณหาค่าตัวแปรของสมการกำลังสอง ให้จัดขวามือของเครื่องหมายเท่ากับให้เป็น 0 แล้วการคำนวณจะมีได้ 3 วิธี คือ โดยวิธีแยกตัวประกอบ โดยวิธีทำให้เป็นกำลังสองสมบูรณ์ และโดยวิธีใช้สูตร
…..การแก้สมการกำลังสองโดยวิธีแยกตัวประกอบ
…..ทำได้โดยการแยกตัวประกอบ (factors) แล้วใช้หลักว่า เมื่อผลคูณของตัวประกอบเป็น 0 (ขวามือขอเครื่องหมายเท่ากับ) แสดงว่า ตัวประกอบบางตัวเป็น 0 หรือทุกตัวประกอบเป็น 0
…..ทำได้โดยการแยกตัวประกอบ (factors) แล้วใช้หลักว่า เมื่อผลคูณของตัวประกอบเป็น 0 (ขวามือขอเครื่องหมายเท่ากับ) แสดงว่า ตัวประกอบบางตัวเป็น 0 หรือทุกตัวประกอบเป็น 0
ตัวอย่างที่ 1 จงหาคำตอบของสมการ 
วิธีทำ………..
……………
…………………………….. ……….#
……….#
วิธีทำ………..
……………
……………………………..
ตัวอย่างที่ 2 จงแก้สมการ… 
วิธีทำ จัดขวามือของเครื่องหมายเท่ากับให้เป็น
…………………….
………………..
……………………………………. ,
, 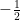 ……….#
……….#
วิธีทำ จัดขวามือของเครื่องหมายเท่ากับให้เป็น
…………………….
………………..
…………………………………….
ตัวอย่างที่ 3 จงแก้สมการ 
วิธีทำ…….
…………
……………………….. ……….#
……….#
วิธีทำ…….
…………
………………………..
ตัวอย่างที่ 4 จงแก้สมการ… 
วิธีทำ จัดสมการใหม่ได้เป็น
………. นำ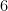 มาคูณทั้งสองข้างของสมการ จะได้
มาคูณทั้งสองข้างของสมการ จะได้
…………………….
…………………….
……………………………………. ,
,  ……….#
……….#
วิธีทำ จัดสมการใหม่ได้เป็น
………. นำ
…………………….
…………………….
…………………………………….
ตัวอย่างที่ 5 จงแก้สมการ… 
วิธีทำ …….. นำ มาคูณทั้งสองข้างของสมการ จะได้
มาคูณทั้งสองข้างของสมการ จะได้
……………..
…………………….
……………..
……………………………… ……….#
……….#
วิธีทำ …….. นำ
……………..
…………………….
……………..
………………………………
ตัวอย่างที่ 6 จงแก้สมการ 
วิธีทำ………
…………..นำ มาหารทั้งสองข้างของสมการ จะได้
มาหารทั้งสองข้างของสมการ จะได้
………………..
…………….
……………………………… ………#
………#
วิธีทำ………
…………..นำ
………………..
…………….
………………………………
ตัวอย่างที่ 7 จงแก้สมการ 
วิธีทำ…….
…………..นำ มาหารทั้งสองข้างของสมการ จะได้
มาหารทั้งสองข้างของสมการ จะได้
…………..
………….
…………………………… …
…
แบบทดสอบเรื่องสมการกำลังสอง
พร้อมเฉลย
จงหาค่าของ x จากสมการต่อไปนี้
1) 4x2 + 12x = 0 ... เฉลยข้อ 1...
2) 3x2 + 9x = 0 ... เฉลยข้อ 2...
3) 4x2 = 16x ... เฉลยข้อ 3...
4) 3x2 = 21x ... เฉลยข้อ 4...
5) 2x2 + 7x = 0 ... เฉลยข้อ 5...
6) 4x2 = 9x ... เฉลยข้อ 6...
7) x2 + 6x + 8 = 0 ... เฉลยข้อ 7...
8) x2 + 11x + 24 = 0 ... เฉลยข้อ 8...
9) x2 + 2x = 15 ... เฉลยข้อ 9...
10) x2 + 2x = 48 ... เฉลยข้อ 10...
11) x2 + 25 = 10x ... เฉลยข้อ 11...
12) x2 = 2x + 15 ... เฉลยข้อ 12...
13) x2 = 5x + 14 ... เฉลยข้อ 13...
14) x2 + 12 = 7x ... เฉลยข้อ 14...
15) x2 + 60 = 17x ... เฉลยข้อ 15...
16) x2 = 9x + 22 ... เฉลยข้อ 16...
17) x2 = 3x + 18 ... เฉลยข้อ 17...
วิธีทำ…….
…………..นำ
…………..
………….
……………………………
แบบทดสอบเรื่องสมการกำลังสอง
พร้อมเฉลย
จงหาค่าของ x จากสมการต่อไปนี้
1) 4x2 + 12x = 0 ... เฉลยข้อ 1...
2) 3x2 + 9x = 0 ... เฉลยข้อ 2...
3) 4x2 = 16x ... เฉลยข้อ 3...
4) 3x2 = 21x ... เฉลยข้อ 4...
5) 2x2 + 7x = 0 ... เฉลยข้อ 5...
6) 4x2 = 9x ... เฉลยข้อ 6...
7) x2 + 6x + 8 = 0 ... เฉลยข้อ 7...
8) x2 + 11x + 24 = 0 ... เฉลยข้อ 8...
9) x2 + 2x = 15 ... เฉลยข้อ 9...
10) x2 + 2x = 48 ... เฉลยข้อ 10...
11) x2 + 25 = 10x ... เฉลยข้อ 11...
12) x2 = 2x + 15 ... เฉลยข้อ 12...
13) x2 = 5x + 14 ... เฉลยข้อ 13...
14) x2 + 12 = 7x ... เฉลยข้อ 14...
15) x2 + 60 = 17x ... เฉลยข้อ 15...
16) x2 = 9x + 22 ... เฉลยข้อ 16...
17) x2 = 3x + 18 ... เฉลยข้อ 17...
แบบฝึกหัดสมการกำลังสอง
สมการกำลังสองที่มีรูปทั่วไปเป็น ax2 + bx + c = 0 เมื่อ a , b , c เป็นค่าคงตัว และ a ไม่เท่ากับ 0 ทำได้โดย
อาศัยการแยกตัวประกอบ หาจำนวนเต็มสองจำนวนที่คูณกันได้ c และบวกกันได้ b ตัวอย่าง จงหาคำตอบของสมการ x2 – 32x + 31 = 0
x2 – 32x + 31 = 0
( x2– 31 ) ( x – 1 ) = 0
ดังนั้น x – 31 = 0 หรือ x – 1 = 0
x = 31 หรือ x = 1
คำตอบของสมการคือ 31 และ 1
ตัวอย่าง จงหาคำตอบของสมการ x2+ 5x + 6 = 0
x2 + 5x + 6 = 0
( x + 2 ) ( x + 3 ) = 0
ดังนั้น x + 2 = 0 หรือ x + 3 = 0
x = -2 หรือ x = -3
คำตอบของสมการคือ -2 และ -3
...........................................................................
ในการแก้สมการบางครั้ง ถ้านำค่าคงตัวมาคูณหรือหารทั้งสองข้างของสมการ จะช่วยให้การแยกตัวประกอบเพื่อหาคำตอบของสมการทำได้ง่ายขึ้น
ตัวอย่าง จงแก้สมการ -6x2 + 12x – 6 = 0
-6x2 + 12x – 6 = 0
นำ -6 มาหารทั้งสองข้างของสมการ จะได้
x2– 2x + 1 = 0
( x – 1 ) ( x – 1 ) = 0
ดังนั้น x – 1 = 0
x = 0
คำตอบของสมการคือ 1
ตัวอย่าง จงแก้สมการ 1.5x2 = 7.7x - 1
1.5x2 - 7.7x + 1 = 0
นำ 10 มาคูณทั้งสองข้างของสมการ จะได้15x2 – 77x + 10 = 0 ( 15x – 2 ) ( x - 5 ) = 0 ดังนั้น 15x – 2 = 0 หรือ x – 5 = 0 x = เศษ 2 ส่วน 15 หรือ 5 คำตอบของสมการคือ เศษ 2 ส่วน 15 และ 5 ..............................................................................
การหาคำตอบของสมการกำลังสองในรูป ax2 + bx + c = 0 เมื่อ a , b , c เป็นค่าคงตัว และ a ไม่เท่ากับ 0 ใน
กรณี c มีค่าเป็น 0 ใช้สมบัติการแจกแจง
ตัวอย่าง จงแก้สมการ 15x2 – 10x = 0
15x2 – 10x = 0
5x2 ( 3x – 2 ) = 0
ดังนั้น 5x = 0 หรือ 3x – 2 = 0
x = 0 หรือ x = เศษ 2 ส่วน 3
คำตอบของสมการคือ 0 และ เศษ 2 ส่วน 3
.........................................................................
การหาคำตอบของสมการกำลังสอง ในรูป ax + bx + c = 0 เมื่อ a , b ,c เป็นค่าคงตัว และ a ไม่เท่ากับ 0 ในกรณีที่ c มีค่าเป็น 0 การแก้สมการกำลังสองที่ได้รูปทั่วไปเป็น x2 = c เมื่อ c > 0 x2 – c = 0
ตัวอย่าง จงแก้สมการ x2 – 169 = 0x2 - 132 = 0 ( x – 13 ) ( x + 13 ) = 0
ดังนั้น x – 13 = 0 หรือ x + 13 = 0
x = 13 หรือ x = -13
คำตอบของสมการคือ 13 และ -13
ตัวอย่าง จงแก้สมการ 4x2 = 16
4x2 - 16 = 0
( 2x )2 – 42 = 0
( 2x – 4 ) ( 2x + 4 ) = 0
ดังนั้น 2x – 4 = 0 หรือ 2x + 4 = 0x = เศษ 4 ส่วน 2 หรือ x = - เศษ 4 ส่วน 2 x = 2 หรือ x = -2 คำตอบของสมการคือ 2 และ -2 ............................................................................. การแก้สมการกำลังสองที่มีรูปทั่วไปเป็น x2 = c เมื่อ c > 0 ตัวอย่าง จงแก้สมการ ( 2x – 3 )2 = 16 ( 2x - 3 )2 - 16 = 0
( 2x - 3 )2 - 42 = 0
( 2x – 3 – 4 ) ( 2x – 3 + 4 ) = 0( 2x + 1 ) ( 2x– 7 ) = 0 ดังนั้น 2x + 1 = 0 หรือ 2x – 7 = 0 2x = -1 หรือ 2x = 7 x = - เศษ 1 ส่วน 2 หรือ x = เศษ 7 ส่วน 2 คำตอบของสมการคือ - เศษ 1 ส่วน 2 และ เศษ 7 ส่วน 2 |
ไม่มีความคิดเห็น:
แสดงความคิดเห็น